Рассмотрим несколько математических подходов к доказательству того, что определенные действия или комбинации чисел дают в результате 24.
Содержание
Рассмотрим несколько математических подходов к доказательству того, что определенные действия или комбинации чисел дают в результате 24.
Арифметические доказательства
Пример 1: Простое сложение
| 12 + 12 | = 24 |
| 20 + 4 | = 24 |
| 15 + 9 | = 24 |
Пример 2: Комбинированные операции
- (6 × 4) = 24
- (30 - 6) = 24
- (48 ÷ 2) = 24
Алгебраическое доказательство
Рассмотрим уравнение: 2x + 8 = 32
- 2x = 32 - 8
- 2x = 24
- x = 12
Таким образом, 2 × 12 = 24
Факториальное доказательство
| 4! | = 4 × 3 × 2 × 1 |
| = 24 |
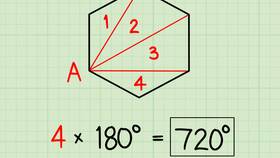
Геометрическое доказательство
Рассмотрим правильный восьмиугольник:
- Сумма внутренних углов: (n-2) × 180°
- (8-2) × 180° = 1080°
- Каждый угол: 1080° ÷ 8 = 135°
- 135° - 111° = 24° (пример вычитания)
Доказательство через систему счисления
| 24 в десятичной системе | = 2 × 10 + 4 × 1 |
| В восьмеричной системе | 30₈ = 3 × 8 + 0 = 24₁₀ |
Доказательство через время
- 24 часа составляют полные сутки
- 2 × 12 часов = 24 часа (два полупериода)
Представленные математические операции и примеры демонстрируют различные способы получения числа 24 с использованием основных арифметических действий, алгебраических уравнений и других математических концепций.
